Rosette Phaser / Multiplier

Rosette Phaser / Multiplier Installed on
an MDF Rose Engine Lathe

Tom Johanson came up with the idea of adding a second drive motor to the MDF Rose Engine Lathe, letting it drive the rotation of the rosettes. By doing this, the spindle drive motor is no longer driving the rosette rotation; only the rotation of the object being turned.

Ed French then added the functionality to use this in version 3.0 of ELFOS (more information about that system is available at the MDF Rose Engine Lathe 2.0 Library).

Together, these deliver these functions for the turner:

multiplication of the rosette's patterns, including making virtual rosettes which would otherwise be impossible to use,
indexing of the rosette, separate from the object held in the spindle (as done using the worm screw on a crossing wheel),
phasing of the rosette (as done using phasing holes on the rosette or a crossing wheel), and
dynamic phasing of the rosette.

Rosette Pattern Multiplication

Oval Rosette

By rotating the rosette at a different speed from the object, the rosette's pattern will be repeated more or less often. For example, if the rosette is rotating at twice the speed of the object, then the effect will be the same as having twice the patterns on the rosette.

The picture to the right shows an oval rosette with three multiplication factors, all using the same starting point (at 9:00 in the picture).

The black line is at 100% (i.e., no multiplication).
The red line is at 50%. At 50%, there is only one lobe on the oval, making it rather circular.
The blue line is at 200%. At 200%, there are four lobes. This looks like two oval rosettes were overlaid at 90° to each other.

Below are some examples using an F-4 rosette:

Actual Rosette = F-4 Speed Differential = 50% Effective Rosette = F-2		Actual Rosette = F-4 Speed Differential = 75% Effective Rosette = F-3
Actual Rosette = F-4 Speed Differential = 100% Effective Rosette = F-4		Actual Rosette = F-4 Speed Differential = 125% Effective Rosette = F-5
Actual Rosette = F-4 Speed Differential = 150% Effective Rosette = F-6		Actual Rosette = F-4 Speed Differential = 200% Effective Rosette = F-8

This opens up opportunities for the turner to have access to previously unavailable rosettes.

Actual Rosette = GDP-3
Speed Differential = 50%
Effective Rosette = GDP-1.5

It takes 2 revolutions to complete the pattern.

Actual Rosette = A-96
Speed Differential = 100%
Effective Rosette = A-96

Actual Rosette = GDP-3
Speed Differential = 100%
Effective Rosette = GDP-3

Actual Rosette = A-96
Speed Differential = 200%
Effective Rosette = A-192

Actual Rosette = GDP-3
Speed Differential = 200%
Effective Rosette = GDP-6

Rosettes with different lobe structures have different amplitudes. For example, an F1 at 400% is very different from an F4 at 100%.

Actual Rosette = F-4
Speed Differential = 100%
Effective Rosette = F-4

Actual Rosette = F-1
Speed Differential = 400%
Effective Rosette = ???

"Impossible" Rosettes

One-Lobed Rosette

Tom was able to demonstrate some really unique features using his One-Lobed Rosette. By running the rosette at 16x the speed of the spindle, the effective result was a rosette which looked like the pattern shown to the left.

16-Lobed Virtual Rosette

Such a pattern of rises and falls would be impossible for a rubber to follow, so this would be a rosette which would be "impossible" to use.

Rosette Indexing

If the turner wants to adjust the rotational alignment of the rosette to the object being turned, there are a number of ways to do that; however the approach here is easiest. The steps would be:

Secure the object in the chuck, and ensure it is aligned properly along the Z axis.
Ensure the cutter is properly aligned, especially along the Y axis.
Rotate the spindle so that the object is set at the desired starting point for cuts.
Index the rosette (relative to the object held in the spindle) so that it is also aligned with the starting point for cutting. This is the new functionality for the MDF Rose Engine Lathe, and is similar to what is provided by the worm screw on a crossing wheel.
Begin cutting ...

An example of where this function would be quite useful is when adding ornamentation to a segmented or staved piece. The piece can be rotated so that the pattern imparted by the rosette would start wherever the turner wanted.

Rosette Phasing

As the rosette can be indexed independently from the spindle, the effect of phasing can be also achieved. This is especially easy when using ELFOS as indexing can be done in divisions of a circle.

For example, if you are using a 7-sided rosette,

1 lobe = ¹/₇^th of a circle
¹/₂ lobe = ¹/₁₄^th of a circle
¹/₄ lobe = ¹/₂₈^th of a circle

Each indexing of the rosette, using 28 divisions of a circle, will achieve indexing the rosette by ¹/₄ lobe.

Dynamic Rosette Phasing

Tudor-8 pattern wrapped
180° around a cylinder

With the historical way in which phasing has been implemented, a series of cuts would be made, and then the rosette would be rotated (phased) relative to the object being cut. This certainly enabled some wonderful artistic effects.

With dynamic phasing, there is no need to stop the cutting before phasing.

An example of where this function would be useful is when cutting along the side of a piece using a linear or curvilinear slide. As the cutter is moved along the piece, the rosette can be phased dynamically. The effect would be to impart the rosette's design helically along the object, similar to screw threads.

The piece shown to the right shows such a pattern of rosette rotation.

Examples of this device in use

Oval Rosette

Tom Johanson did some testing surrounding the multiplication of the rosette's patterns. His tests were to try various options on the multiplication percentage when using an oval rosette. The oval rosette was chosen as its pattern collapses when the cut radius is small. This can be seen in the paper chuck drawing of an oval rosettes's pattern, shown to the right.

In this testing, the relationship of the rosette to the spindle's speed is reflected in the table below. All the drawings were made at a small diameter, with the same pen setting, and the same amplitude adjustment (100%).

What was found is that the percentage selection can drive an increase or decrease in the number of lobes (as noted above). Where there is an integer number of lobes, the results were shown in the table below on a row basis.

The columns in the table below, the number of revolutions, represents the full revolutions required to complete the pattern.

	Revolutions
	1	2	3	4	5	6	7	8 1 Lobe
1 Lobe	50%	25%	16.667%	12.5%	10%	8.333%	7.1429%	6.25% 2 Lobes
2 Lobes	100%	*n/a* 50% = 1 lobe, 1 revolution	33.333%	*n/a* 25% = 1 lobe, 2 revolutions	20%	*n/a* 16.667% = 1 lobe, 3 revolutions	14.286%	*n/a* 12.5% = 1 lobe, 4 revolutions 3 Lobes
3 Lobes	150%	75%	*n/a* 50% = 1 lobe, 1 revolution	37.5%	30%	*n/a* 25% = 1 lobe, 2 revolutions	21.429%	18.75% 4 Lobes
4 Lobes	200%	*n/a* 100% = 2 lobes, 1 revolution	66.67%	*n/a* 50% = 1 lobe, 1 revolution	40%	*n/a* 33.333% = 2 lobes, 2 revolutions	28.571%	*n/a* 25% = 1 lobe, 2 revolutions 5 Lobes
5 Lobes	250%	125%	83.333%	62.5%	*n/a* 50% = 1 lobe, 1 revolution	41.667%	35.714%	31.25% 6 Lobes
6 Lobes	300%	*n/a* 150% = 3 lobes, 1 revolution	*n/a* 100% = 2 lobes, 1 revolution	*n/a* 75% = 3 lobe, 2 revolutions	60%	*n/a* 50% = 1 lobe, 1 revolution	42.857%	*n/a* 37.5% = 3 lobe, 4 revolutions 7 Lobes
7 Lobes	350%	175%	116.667%	87.5%	70%	58.33%	*n/a* 50% = 1 lobe, 1 revolution	43.75% 8 Lobes
8 Lobes	400%	*n/a* 200% = 4 lobes, 1 revolution	133.33%	*n/a* 100% = 2 lobes, 1 revolution	80%	*n/a*' 66.67% = 4 lobes, 3 revolutions	57.143%	*n/a* 50% = 1 lobe, 1 revolution 9 Lobes
9 Lobes	450%	225%	*n/a* 300% = 6 lobes, 1 revolution	112.5%	90%	*n/a* 75% = 3 lobes, 2 revolutions	64.286%	56.23% 10 Lobes
10 Lobes	500%	*n/a* 250% = 5 lobes, 1 revolution	166.67%	*n/a* 125% = 5 lobes, 1 revolutions	*n/a* 100% = 2 lobes, 1 revolution	*n/a* 83.33% = 5 lobes, 3 revolutions	71.429%	*n/a* 62.5% = 5 lobes, 4 revolutions

To generalize what was found, for a given number of Lobes(L),

M3Speed_L = Lobes × 50%

There are solutions also at harmonic values to this speed. So, for a given harmonic value (H),

M3Speed_LH = M3Speed_L ÷ H

What was also found is that the number of revolutions (R) required to complete the pattern equals the harmonic.

R = H

5 Lobes
3d Harmonic

So, if you want 5 lobes with a design at the 3rd harmonic, the speed of M3 would need to be:

L = 5

H = 3

R = 3

M3Speed_L5 = 5 × 50%

M3Speed_L5 = 250%

M3Speed_L5H3 = 250% ÷ 3

M3Speed_L5H3 = 83.33%

Where there are blank cells in this table, there is no good solution. For example, there are desired solutions such as:

L = 3

H = 3

M3Speed_L3 = 3 × 50%

M3Speed_L3 = 150%

M3Speed_L3H3 = 150% ÷ 3

M3Speed_L3H3 = 50%

1 Lobe
1st Harmonic

In theory that should work; however we also know that 50% yields a 1 Lobe object at the 1st harmonic.

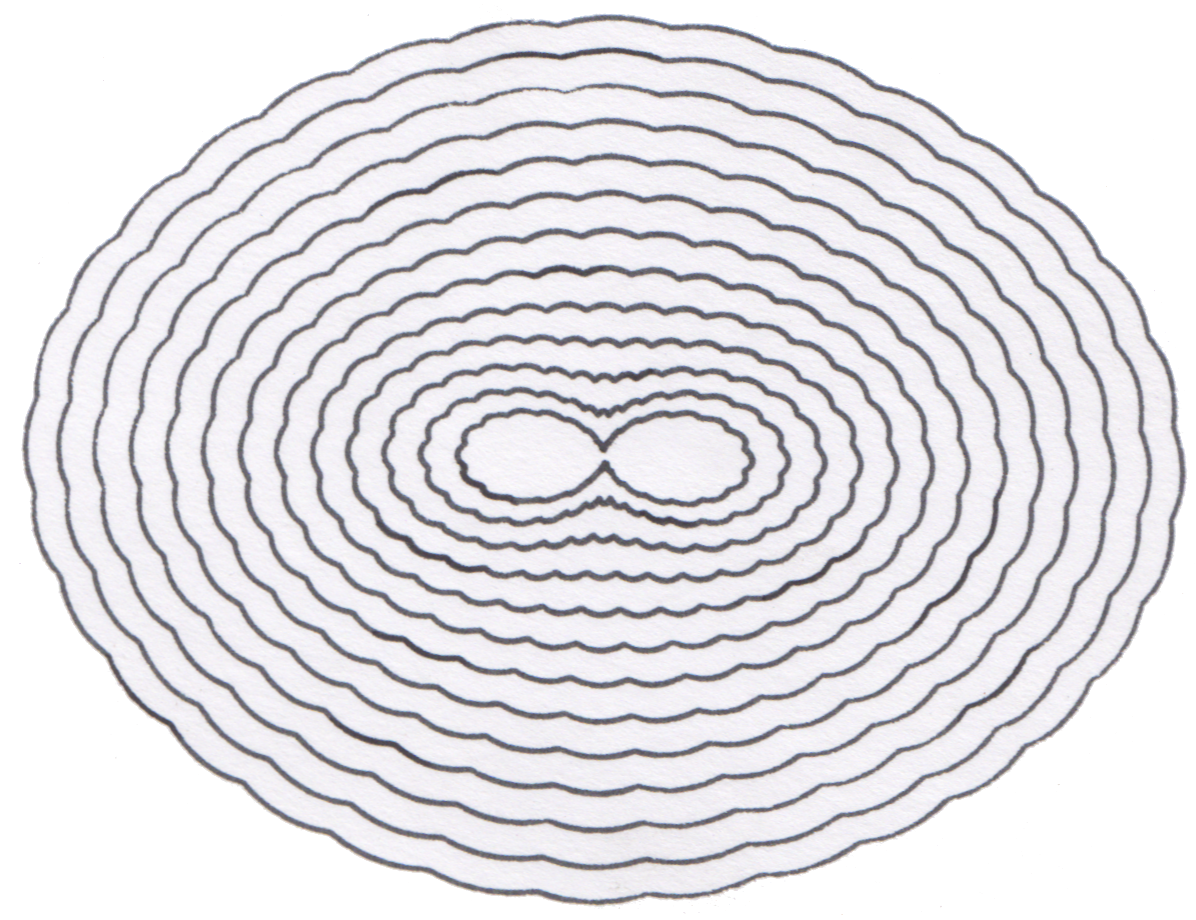
Bumpy Ellipse Rosette

Tom Johanson then ran a subset of this test again using the Bumpy Ellipse rosette.

What is greatly interesting here is how, at 11 and 12 revolutions, the bumps on the rosette become lobes in the design.

Revolutions
	1	2	3	4	5	6 5 Lobes
5 Lobes	250%	125%	83.33%	62.5%	*n/a*	41.666%

Revolutions
	7	8	9	10	11	12 5 Lobes
5 Lobes (cont'd)	35.714%	31.25%	27.777%	*n/a*	22.727%	20.833%

Usage Notes

Phasing a Rosette's Design

Phasing of the design can be achieved by:

Indexing the rosette whilst keeping the spindle fixed, or
Indexing the spindle whilst keeping the rosette fixed.

It is recommended that you pick one approach and always use that one. This will develop muscle memory and make repeatability easier. Otherwise it would be too easy to make a mistake.

Phasing a Virtualized Rosette's Design

When using rosette multiplication, the indexing for phasing is different when indexing the rosette than when indexing the spindle.

Example
For this example, an 8-sided rosette will be virtualized to be 7-sided by rotating the rosette at ⁷/₈ speed (87.5%) of the spindle. The spindle (and the object) continues to run at 100%.

	Speed	Lobes in 360°	Full Lobe		Half Lobe
	Speed	Lobes in 360°	Degrees	Divisions of a Circle	Degrees	Divisions of a Circle
Rosette	87.5%	8 lobes	45°	8	22.5°	16
Spindle	100.0%	7 lobes	~51.4286°	7	~25.7143°	14

Phasing of the design half a lobe can be achieved by:

indexing the rosette, using 16 divisions of a circle or 22.5°, or
indexing the spindle (i.e., the object), using 14 divisions of a circle or 25.7142857143°.

The recommended approach is to always index the rosette. This way, any virtualization to achieve a different number of lobes can be ignored.

Indexing with ELFOS

When using ELFOS, be certain indexing is set the way you want.

For certain operations, you will want to have the spindle and M3 synchronized so that the index operation rotates both simultaneously. In those cases, be sure the Synchro is set to on.
If you are wanting to use the Index function to phase only the rosette (and not the spindle), then the spindle and M3 should not be synchronized. In those cases, be sure the Synchro is set to off.

How it works

This YouTube video overviews what it is, how it is attached to the rose engine lathe, and discusses how it works.

Notes on making one

The instructions for making one are in a manual at the MDF Rose Engine Lathe 2.0 Library. There is a red book there titled, Jigs, Fixtures, & Add-Ons.

About this Site

Disclaimer: eMail comments to me at OTBookOfKnowledge @ Gmail.com. The process of woodturning involves the use of tools, machinery and materials which could cause injury or be a health hazard unless proper precautions are taken, including the wearing of appropriate protective equipment.

Rosette Phaser / Multiplier

Rosette Pattern Multiplication

"Impossible" Rosettes

Rosette Indexing

Rosette Phasing

Dynamic Rosette Phasing

Examples of work produced with this device

Examples of this device in use

Usage Notes

Phasing a Rosette's Design

Phasing a Virtualized Rosette's Design

Indexing with ELFOS

How it works

Notes on making one

More Information

Published Articles

Books and Papers

Web Sites

Presentations

Other